Du neurone à l’intelligence artificielle ?

Premier article sur le domaine de l’intelligence artificielle et les liens avec la neuroscience, j’ai choisi de présenter ici le concept du réseau de neurones artificiels, largement utilisé dans le domaine. Ce modèle fait référence à deux notions clés : le neurone formel et la loi de Hebb.

Réseau de neurones ?

Le réseau de neurones artificiels est un modèle largement utilisé dans le domaine de l’intelligence artificielle et notamment la reconnaissance de formes. Ce modèle formel est dérivé du modèle biologique : le neurone du cerveau.  Pour  rappel, le neurone est cellule nerveuse dotée d’un corps cellulaire et de ramifications nommées dendrites où circule l’information sous forme d’impulsion électrique. Il traite l’information puis transmet le résultat aux autres neurones avec son axone (ou fibre nerveuse). Le signal sera émis vers d’autres neurones grâce aux synapses.

Le neurone formel

Le neurone formel (ou neurone artificiel) a été proposé dès les années 1940 par Mc Culloch et Pitts, tous deux mathématiciens. Ils donnent la première définition du neurone formel en s’appuyant sur les propriétés des neurones biologiques : il s’agirait d’une unité pouvant avoir deux états possibles (0 ou 1, respectivement au repos ou excité) comme une unité de traitement logique dont la sortie vaut 0 ou 1. La modélisation neuronale sous forme de synoptique est la suivante :

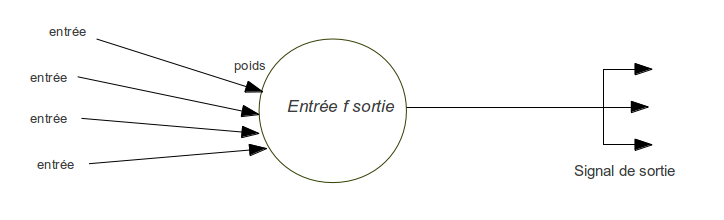
Le neurone intègre des entrées (stimuli) dont la force est plus ou moins importante. Le neurone effectue une opération avec des entrées en vue de générer une sortie. Cette sortie est ensuite transférer à son réseau (i.e. les neurones avec lesquels celui-ci est connecté).

La loi de Hebb

Une autre notion importante à connaître est la théorie Hebbienne de 1949 qui est notamment à la base du concept de la plasticité neuronale. L’apprentissage et la mémoire implique des évolutions au niveau des neurones et synapses notamment une densification synaptique des aires cérébrales concernées par l’apprentissage. Cela est important pour comprendre ensuite comment notre réseau de neurones artificiels apprend ce pour quoi il a été développé.

De manière plus précise, la loi de Hebb exprime la loi de contiguité neuronale : « neurons that fire together, wire together » … Deux zones corticales sont stimulées simultanément à plusieurs reprises, après un certain nombre d’itérations, il suffit d’appliquer l’un des stimuli, ou signaux d’entrées, pour que les zones corticales associées soient automatiquement excitées (passage de 0 à 1).

Cette loi est importante lorsque l’on considère non plus le neurone au niveau individuel mais le neurone dans son écosystème qu’est le réseau.

Du neurone au réseau de neurones : ça se corse !

Un réseau de neurones est une interconnexion totale ou partielle de neurones formels. Il émerge un comportement de ce réseau notamment l’apprentissage (une forme d’intelligence collective).

Il existe plusieurs modèle de réseaux selon l’interconnexion des neurones (le type et le nombre de connexions). Les connexions entre les neurones dans les réseaux sont appelés synapses. Il existe trois grands types de connexions :

• Le réseau partiellement connecté : les neurones ne sont pas tous connectés entre eux, ils sont connectées avec ceux avoisinants,
• Le réseau à connexion complète : tous les neurones sont interconnectés,
• Le réseau à couches : Les neurones sont répartis en couches. Tous les neurones d’une couche sont connectés aux neurones de la couche précédente.

L’information et son transport dans un réseau de neurones réside dans la configuration de celui-ci comme le nombre de neurones, de couches, le nombre de liens avec eux. Le poids synaptique est aussi un facteur important qui représente la force des connexions entre les neurones (comme dans notre cerveau). L’information est transportée avec plus ou moins de force et a une action inhibitrice ou excitatrice. La fonction d’activation joue également un rôle qui détermine la réaction du neurone en fonction de l’information reçue.

En fonction des caractéristiques du réseau de neurones, il permet de modéliser deux niveaux d’apprentissage :

• Modèle d’apprentissage supervisé : La forme à reproduire par le réseau neuronal est présentée aux entrées et ce qu’on voudrait obtenir aux sorties (nous parlons alors de « réseau à apprentissage supervisé » dans ce cas),
• Modèle d’apprentissage non supervisé : Une entrée est présentée au réseau et celui-ci évolue jusqu’à se rapprocher de la forme (= réseau à apprentissage non supervisé).

Nous verrons dans les prochains articles des exemples d’application de ces principes.